内容提要: 不过就是各种流量相等而已

首先介绍梯度、散度和旋度：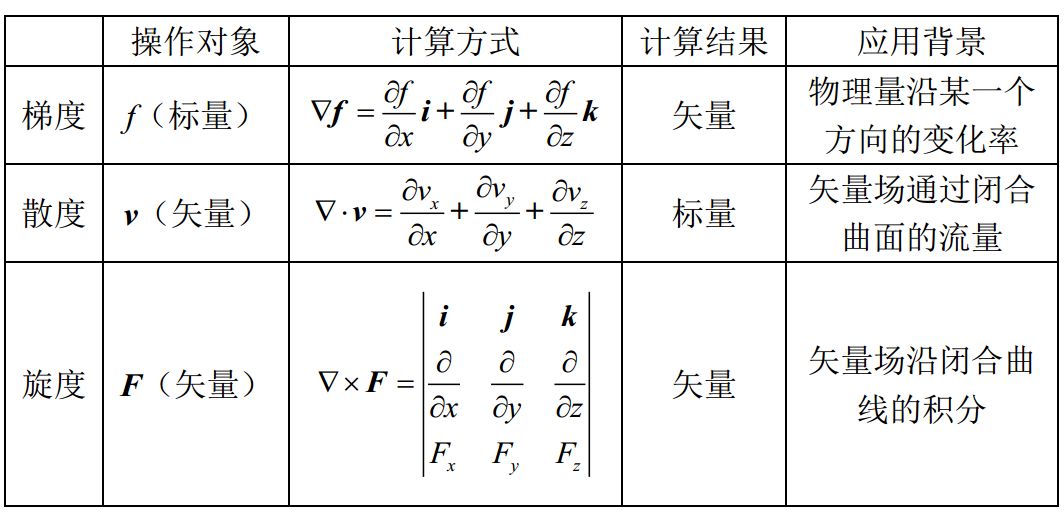

有了上面的基础，今天就以不可压缩流体为例来看看，流体力学里面的连续性方程和 Navier-Stokes 方程到底是啥意思？

连续性方程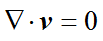

Navier-Stokes 方程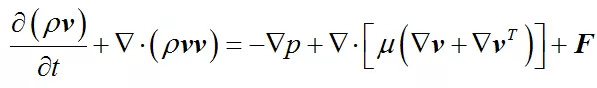

连续性方程

简单来说，连续性方程就是质量守恒定律在流体力学中的具体表述形式。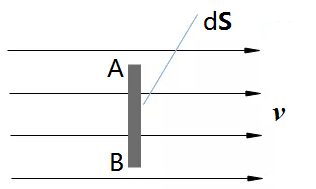

如上图所示，假设流体流动速度为 v 且与平面 AB 垂直，考虑图中的平面 AB，则在 dt 的时间内，通过平面 AB 的质量流量 dΦ为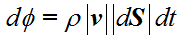

其中的ρ表示流体密度。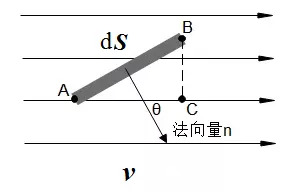

进一步，如果速度 v 和平面 AB 的方向不垂直，而是存在一个夹角θ，则在 dt 的时间内，通过这个平面的质量流量 dΦ就成了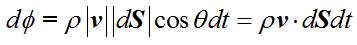

对于一个闭合曲面而言，我们只需对每一个平面微元的质量流量进行求和，即可得到在 dt 时间内流体通过该闭合曲面的质量流量Φ为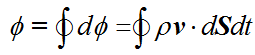

也就是说：

因为流体流动，流出闭合曲面的流体质量为Φ。反之，流入闭合曲面的流体质量为 -Φ。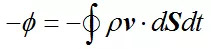

此外，闭合曲面内流体的质量为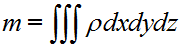

在 dt 的时间内，闭合曲面内流体的质量增加量 dm 为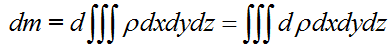

由于流体质量守恒，流体的质量增加量 dm 就应当等于流入闭合曲面的流体质量 -Φ。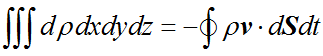

变形整理一下就是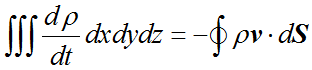

根据散度的定义，有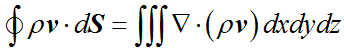

因此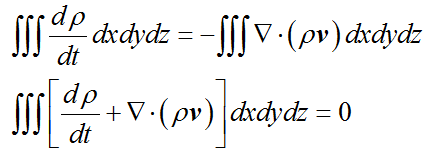

因为流体密度ρ除了是时间 t 的函数以外，还是位置 x,y,z 的函数，所以这里用偏导数代替导数，得到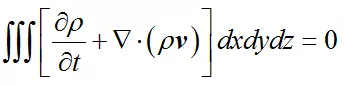

也就是说，对于任意区域来说，流体质量的增加量就等于流入该区域的流体质量。

换算到单位体积（其实就是去掉积分符号），自然就得到了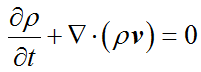

这就是我们平时见到的连续性方程。

进一步，如果流体不可压缩，那流体密度ρ就成了常数且不随时间发生变化，因此连续性方程就简化为了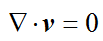

Navier-Stokes 方程

类比连续性方程，我们自然也可以知道，对于任意区域来说，流体动量的增加量就等于流入该区域的流体动量。

质量表达式为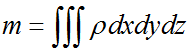

动量表达式为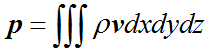

也就是说，动量与质量相比，也就是多乘了个 v 而已。

所以动量守恒方程就变成了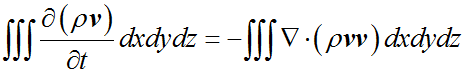

这比 Navier-Stokes 方程方程简单太多了，你这是错的吧！

的确，以上情况只在流体完全不受力的情况下成立。

牛顿爵士告诉我们，动量为 p 的质点，在外力 F 的作用下，其动量随时间的变化率等于该质点所受的外力。

也就是说，除了流入该区域的流体动量，流体区域内所受的力也会造成流体动量的变化。

其中一定存在的力有两个，一个是压力，而另一个就是粘性力。压力主要用于平衡流体之间的受力，而粘性力则是由于流体的流动而引起的。对于不可压缩流体而言，它们的大小就等于

由于推导实在是太过复杂，这里就不详细推导了。我们直接把前人的结果拿来用就好了。想具体了解的同学可以参考周光坰流体力学上册的 1.6 和 4.5 节。

至于其他力，比如说重力，电磁力等等，既然没有表达式，不妨直接把它们写到一起，记做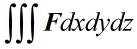

力的存在效果和流入该区域的动量是等价的，因此 N-S 方程最终就成了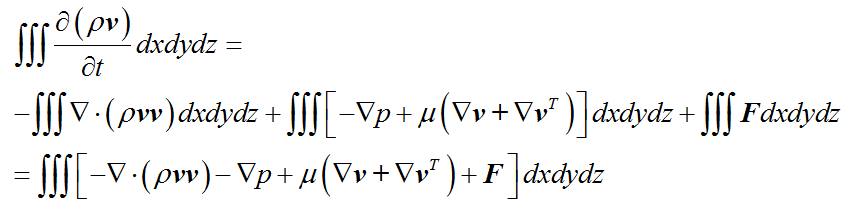

也就是说，对于任意区域来说，流体动量的增加量就等于流入该区域的流体动量加上该区域所受的力。

换算到单位体积（其实就是去掉积分符号），自然就得到了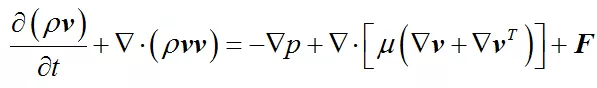

这就是我们平时见到的 Navier-Stokes 方程。

万物流量皆相等（我瞎编的）

事实上，以上推导逻辑可以应用到任何关于流动的场景。

对于任意变量Φ，最终的方程基本上都可以写成：

物理量的增加量 = 物理量的流入量 + 引起物理量增加的其他原因。

变成公式（其实就是把连续性方程的密度ρ换成变量Φ）就是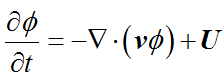

里面的 U 表示 unkown，意思是我也不知道它是个啥。

是不是还挺有意思的，大家快都来学习流体力学吧！